In fact this first version of these notes is just a hastily constructed pastiche of this material which we will improve on (and expand) during the semester.
It is assumed that the student has had an exposure to topology, including at least basic definitions and a few examples in algebraic topology such as the fundamental group and homology groups.
In the next Chapter we introduce the idea of manifold as a subset of ![]() .For completness, here are some basic definitions for refenence as well as to establish notations:
.For completness, here are some basic definitions for refenence as well as to establish notations:
Definition 7366
We define n-dimensional space, denoted ![]() , to be
the set of all ordered n-tuples of real numbers, together with a notion of
distance,
, to be
the set of all ordered n-tuples of real numbers, together with a notion of
distance, ![]() .
If
.
If ![]() and
and ![]() are two points of
are two points of ![]() , the distance between these points denoted by
, the distance between these points denoted by ![]() and defined
by
and defined
by ![]()
Definition 7383
Let ![]() , and
, and ![]() be a given number,
be a given number, ![]() . Then the open n-dimensional ball in
. Then the open n-dimensional ball in ![]() with center
p and radius
with center
p and radius ![]() is defined to be the set
is defined to be the set ![]() ,
, ![]() . We denote this set by
. We denote this set by ![]() . We also refer to
. We also refer to ![]() as an
as an ![]() -neighborhood
of p in
-neighborhood
of p in ![]() .
.
More generally we have
Definition 7396
Let X be a subset of ![]() with
with ![]() .
Given a number
.
Given a number ![]() , with
, with ![]() , we define an
, we define an ![]() -neighborhood of p in X to be the subset of X,
-neighborhood of p in X to be the subset of X, ![]() ,
, ![]() .
.
Definition 7407
If ![]() and
and ![]() is a number,
is a number, ![]() , then the
closed n-dimensional ball with center p and radius
, then the
closed n-dimensional ball with center p and radius ![]() is defined to be
is defined to be ![]() . We denote this set by
. We denote this set by ![]() , or sometimes,
, or sometimes, ![]() .
.
Definition 7432
Let ![]() be numbers with a < b. The following subsets are all called intervals:
be numbers with a < b. The following subsets are all called intervals:
Definition 7439
Let ![]() . We say that A is dense in X if every open subset of X contains a point of A.
. We say that A is dense in X if every open subset of X contains a point of A.
Example 7447
Let Q denote the rational numbers, and Z denote the irrational numbers. Then Q and Z are dense in ![]() .
. ![]()
Remark 7464
It is sometimes useful to note that any subset of ![]() has a countable dense subset. Let in
has a countable dense subset. Let in ![]() , let
, let ![]() be the set of all open neighborhoods,
be the set of all open neighborhoods, ![]() where
where ![]() is a rational number and each of the n coordinates of p is a rational number;
is a rational number and each of the n coordinates of p is a rational number; ![]() will have countably many elements.
For each
will have countably many elements.
For each ![]() , chose one point, call it
, chose one point, call it ![]() , of
, of ![]() , (if this set is non-empty). Then
, (if this set is non-empty). Then ![]() will be a countable subset of X, and one can verify that it is a dense subset of X.
will be a countable subset of X, and one can verify that it is a dense subset of X.
![]()
The definition of limit point is not completely standard. Here is what we will use:
Definition 7478
Let ![]() ,
, ![]() . We
is say that x is a limit point of A in X if every open subset, U, of X
which contains x contains a point of
. We
is say that x is a limit point of A in X if every open subset, U, of X
which contains x contains a point of ![]() . (That is, U contains a
point of A other than x.)
. (That is, U contains a
point of A other than x.)
Here are some useful subsets of ![]()
 |
Definition 7493
We define n-dimensional half space to be:
![]() . (See Figure 0-1).
. (See Figure 0-1).
Definition 7497
We define open n-dimensional half space to be:
![]() . (See Figure 0-1).
. (See Figure 0-1).
For certain subsets of ![]() , generalized cylindrical coordinates may be more convenient. Here we locate points of
, generalized cylindrical coordinates may be more convenient. Here we locate points of ![]() using polar coordinates in the first two coordinates, Cartesian coordinates for the rest.
using polar coordinates in the first two coordinates, Cartesian coordinates for the rest.
Definition 7504
Cylindrical coordinates for ![]() are
are ![]() where
where ![]() .
.
As with polar coordinates, points have multiple descriptions such as
![]() and (0,0,2,3) = (0,1,2,3).
and (0,0,2,3) = (0,1,2,3).
 |
Definition 7515
For an angle, ![]() , the subset
, the subset
![]() is defined, using generalized cylindrical coordinates,
is defined, using generalized cylindrical coordinates, ![]() . Such a subset is called an (n-1)-dimensional page of
. Such a subset is called an (n-1)-dimensional page of ![]() .
.
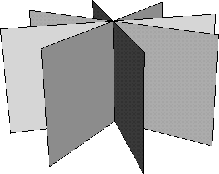
Example 7527
Figure 0-2 we indicate eight pages , H20, ![]() ,
, ![]() ,
,![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() in
in ![]() . Only a square on each page is shown. The term ``page'' comes from the following image--if we take a book and open all the way until the front cover meets the back cover
the pages of the book will fan out and look something like Figure 0-2.
. Only a square on each page is shown. The term ``page'' comes from the following image--if we take a book and open all the way until the front cover meets the back cover
the pages of the book will fan out and look something like Figure 0-2.
![]()
Definition 7533
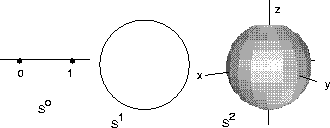
We define the n-dimensional sphere to be the subset
![]() where
where ![]() denotes the origin of
denotes the origin of ![]() . (See Figure 0-3).
. (See Figure 0-3).
 |
Definition 7545
The standard n-ball ( sometimes called the unit n-ball) in ![]() is the set
is the set
![]() . (See Figure 0-4).
. (See Figure 0-4).
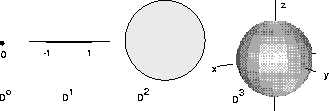 |
Remark 7571
So, S1 is the unit circle in the plane; S2 is the standard unit
sphere in space. Also, S0 consists of two points-the numbers -1 and 1 of
Also, D1 is the closed interval [-1, 1] in ![]() , (see Figure 0-3).
, (see Figure 0-3).
![]() , D2 is the unit disk in the plane, D3 the unit ball in
, D2 is the unit disk in the plane, D3 the unit ball in ![]() , see Figure 0-4 and, for any n,
, see Figure 0-4 and, for any n, ![]() .
. ![]()
Definition 7582
The standard n-simplex in ![]() , denoted
, denoted ![]() , is defined by
, is defined by ![]()
![]() with
with ![]() for all i,
for all i, ![]()
![]() .
.
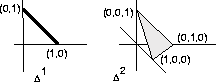 |
Example 7607
standard 1-simplex in the plane is a line segment with endpoints (1,0)
and (0,1).
It is the portion of the line with equation x1 + x2 = 1 which lies in the first quadrant of the plane where ![]() and
and ![]() .
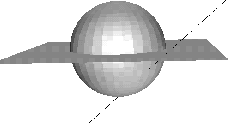
The standard 2-simplex in space is a (two-dimensional) triangle
with vertices (1, 0, 0), (0, 1, 0) and (0, 0, 1), since it is the portion of the plane x1 + x2 + x3 = 1 contained in the first octant of three-dimensional space, (see Figure 0-5).
.
The standard 2-simplex in space is a (two-dimensional) triangle
with vertices (1, 0, 0), (0, 1, 0) and (0, 0, 1), since it is the portion of the plane x1 + x2 + x3 = 1 contained in the first octant of three-dimensional space, (see Figure 0-5).
 |
Here is an important example of a homeomorphism see Figure 0-6.
Proposition 7634
Let Sn be the standard sphere in ![]() and let
and let ![]() be the point
be the point ![]() . Then
. Then ![]() is homeomorphic to
is homeomorphic to ![]() .
.
In fact this homeomorphism can be described as follows: let ![]() and let lx be the line in
and let lx be the line in ![]() containing x and P. Identify
containing x and P. Identify ![]() as a coordinate hyperplane of
as a coordinate hyperplane of ![]() as its image, under the standard inclusion map. Then h(x) is defined to be the intersection of the line lx and the hyperplane
as its image, under the standard inclusion map. Then h(x) is defined to be the intersection of the line lx and the hyperplane ![]() . The map h is called stereographic projection.
. The map h is called stereographic projection.
Proof: Suppose ![]() ,
, ![]() .In vector notation we can write lx as
.In vector notation we can write lx as ![]() . In term of coordinates this is:
. In term of coordinates this is:
![]()
The intersection we want is the point on lx, where the last coordinate is zero. This happens if ![]() .
.
Thus we see that
![]()
Using this formulation, we can now verify that h is, in fact, a homeomorphism.
width4pt height6pt depth1.5pt
In the next definitions, we use vector notation for ![]() . If M is an
. If M is an ![]() matrix
matrix ![]() is matrix multiplication where we write the m-dimensional vector,
is matrix multiplication where we write the m-dimensional vector, ![]() , as a single column matrix.
Also |M| denotes the determinant of a square matrix..
, as a single column matrix.
Also |M| denotes the determinant of a square matrix..
Definition 7663
If M is an ![]() matrix and
matrix and ![]() is an n-dimensional vector, we can define a function
is an n-dimensional vector, we can define a function ![]() by
by ![]() .
Such a function is called an affine transformation or affine map.
In the case that m=n, and
.
Such a function is called an affine transformation or affine map.
In the case that m=n, and ![]() , then we say that F is a non-singular affine map.
, then we say that F is a non-singular affine map.
An affine map with ![]() is called a linear transformation or linear map. A non-singular affine map with
is called a linear transformation or linear map. A non-singular affine map with ![]() is called a non-singular linear transformation or non-singular linear map
is called a non-singular linear transformation or non-singular linear map
Remark 7670
An affine map ![]() is simply a function of the form f(x) = m x +b; f is non-singular means
is simply a function of the form f(x) = m x +b; f is non-singular means ![]() .
.
A critical definition we use here, common in linear algebra, is that of an orthogonal matrix. Here MT denotes the transpose of M, that is if M = [ai j], then MT = [aj i].
Definition 7680
Let M be an ![]() matrix. We say M is an orthogonal matrix if
MT = M-1.
matrix. We say M is an orthogonal matrix if
MT = M-1.
Remark 7698
We establish a few properties of an orthogonal matrix.
If M is an orthogonal matrix, then M-1 is also orthogonal. If M is orthogonal, then MT = M-1. Take the transpose of both sides of this equation, and we get M = (M-1)T. Since M is the inverse of M-1, this last equation can be written (M-1)-1 = (M-1)T, which verifies that M-1 is orthogonal.
If M is an orthogonal matrix, then the determinant of M is +1 or -1.
We have MT M = I. But ![]() , so taking the determinant of both sides of the previous equation, and since the determinant of the product is the product of the determinants, we get
, so taking the determinant of both sides of the previous equation, and since the determinant of the product is the product of the determinants, we get ![]() , thus
, thus ![]() .
. ![]()
Definition 7704
An affine map ![]() defined by
defined by ![]() is called a rigid motion of
is called a rigid motion of ![]() , if M is an orthogonal matrix.
, if M is an orthogonal matrix.
Example 7729
If
The matrix
Next some examples in
The matrix
![]() ,
, ![]() , function
, function ![]() corresponds to a counter-clockwise rotation of angle
corresponds to a counter-clockwise rotation of angle ![]() about the origin.
The inverse of M corresponds to clockwise rotation of angle
about the origin.
The inverse of M corresponds to clockwise rotation of angle ![]() , with matrix
, with matrix ![]() . Thus M is orthogonal.
. Thus M is orthogonal.
![]() corresponds to reflection in the x-axis, while
corresponds to reflection in the x-axis, while ![]() corresponds to reflection in the y-axis.
corresponds to reflection in the y-axis.
![]() . The matrix
. The matrix
![]() . Similarly
. Similarly
![]() about the y axis.
about the y axis.
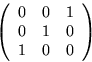
![]()
In the term ``rigid motion'' ``rigid '' refers to the fact is that distances are preserved as the next proposition shows.
Proposition 7736
Suppose we have a rigid motion, F, in ![]() . If
. If ![]() are two vectors in
are two vectors in ![]() then
then
![]()
Proof: Recall that
![]()
Write ![]() . Then,
. Then,
![]()
![]()
![]()
![]()
![]()
Taking square roots it follows that
![]() .
width4pt height6pt depth1.5pt
.
width4pt height6pt depth1.5pt
Here are two standard constructions we will use several times in this book.
Definition 7753
Suppose ![]() and let
and let ![]() be a point whose last coordinate is non-zero. Then the cone on X from p is the union of all line segments in
be a point whose last coordinate is non-zero. Then the cone on X from p is the union of all line segments in ![]() from p to a point of X.
from p to a point of X.
Definition 7767
Suppose ![]() and let
and let ![]() be a points with the last coordinate of p is positive
the last coordinate of q is negative. Then the suspension of X from p and q is the union of all line segments in
be a points with the last coordinate of p is positive
the last coordinate of q is negative. Then the suspension of X from p and q is the union of all line segments in ![]() from p to a point of X and from q to a point of X.
from p to a point of X and from q to a point of X.
Example 7771
we consider ![]() , then the cone from any point is, geometrically, a cone.
, then the cone from any point is, geometrically, a cone.
![]()
If we have ![]() , the concept of closure gives us a way of associating to A a (possibly larger) closed subset of X. The next definition is a way of associating to A a (possibly smaller) open subset of X.
, the concept of closure gives us a way of associating to A a (possibly larger) closed subset of X. The next definition is a way of associating to A a (possibly smaller) open subset of X.
Definition 7792
Suppose ![]() ; we say a is an interior point of A in X, if there is an open subset, U, of X with
; we say a is an interior point of A in X, if there is an open subset, U, of X with ![]() .
.
The subset of A consisting of all interior points of A is called the interior of A. This is denoted by int(A,X). As with closure, if the set X is understood in context, one often uses the notation int(A).
Proposition 7807
Suppose ![]() then
then
Remark 7814
Open subsets can be defined in terms of interior points. It follows from Proposition 0.32 that if ![]() , U is an open subset of X if and only if every point of U is an interior point of U.
, U is an open subset of X if and only if every point of U is an interior point of U.
![]()
Definition 7828
Suppose ![]() ; we say a is a boundary point of A in X if
; we say a is a boundary point of A in X if ![]() . (Note: the closures are closures in X.)
. (Note: the closures are closures in X.)
The set of boundary points of A in X is called the boundary of A in X, denoted Bd(A).
Remark 7834
If ![]() , then the boundary of A is a closed subset of X, since it is the intersection of closed subsets.
, then the boundary of A is a closed subset of X, since it is the intersection of closed subsets.
![]()
Proposition 7840
If ![]() , then the interior of A and the boundary of A are disjoint sets, whose union is A.
width4pt height6pt depth1.5pt
, then the interior of A and the boundary of A are disjoint sets, whose union is A.
width4pt height6pt depth1.5pt
Here are a few basic facts relating closure, boundary and interior of a subset to Cartesian products.
Proposition 7848
Suppose ![]() and
and ![]() then
then
Remark 7855
If A and B are closed subsets then ![]() and so the first formula of Proposition 0.37 c) simplifies to the more easily remembered:
and so the first formula of Proposition 0.37 c) simplifies to the more easily remembered:
![]()
![]()
 |
Example 7881
The formulas of Proposition 0.37 c) would benefit from an example. Suppose A is the closed unit disk in
Since A and B are closed subsets, we may use the simplified formula of Remark 0.38.
![]() and B is the unit interval in
and B is the unit interval in ![]() . Then Bd(A) is the unit circle and Bd(B) is a two point set consisting of the two numbers 0 and 1.
. Then Bd(A) is the unit circle and Bd(B) is a two point set consisting of the two numbers 0 and 1.
![]() is a cylindrical solid in
is a cylindrical solid in ![]() and
and
![]() is the ``surface of the cylindrical solid'', see Figure 0-7, upper left. Note
is the ``surface of the cylindrical solid'', see Figure 0-7, upper left. Note ![]() is the union of the cylindrical surface,
is the union of the cylindrical surface, ![]() , which is the ``side of the solid cylinder'', Figure 0-7, upper right, and
, which is the ``side of the solid cylinder'', Figure 0-7, upper right, and ![]() , the two disks comprising the top and bottom , Figure 0-7, lower left.
The intersection
, the two disks comprising the top and bottom , Figure 0-7, lower left.
The intersection ![]() consists of two disjoint circles.
consists of two disjoint circles. ![]()
Definition 7893
Suppose ![]() ,
, ![]() and
and ![]() are paths in X with f(1) = g(0). Define a path
are paths in X with f(1) = g(0). Define a path
![]() in X called the concatenation of f and g by
in X called the concatenation of f and g by
![]()
This final example of this Chapter, especially for the irrational angle case, is an interesting, non-trivial one. In a future Chapter, we will re-state the problem with a new perspective, Example 0.44.
Example 7989
Let C denote the unit circle in the plane, and let
We first note that
Thus, if
Find an integer N so that
We have shown that x0 is a limit point of
Suppose
Definition 7978
The composition
Definition 7987
Suppose ![]() be the set of points of C corresponding to all multiples of a given angle
be the set of points of C corresponding to all multiples of a given angle ![]() . That is, write
. That is, write
![]() and let
and let ![]() , N the natural numbers.
, N the natural numbers.
![]() will be a finite set if and only if
will be a finite set if and only if
![]() is a rational multiple of
is a rational multiple of ![]() . Suppose
. Suppose ![]() is a rational multiple of
is a rational multiple of ![]() and write
and write ![]() , where p and q are positive integers, the fraction written in reduced form. Then
, where p and q are positive integers, the fraction written in reduced form. Then ![]() will consist of q points:
will consist of q points: ![]() . Conversely, if
. Conversely, if ![]() is finite, there there must be a p and a q such that
is finite, there there must be a p and a q such that ![]() and
and ![]() .
.![]() is an irrational multiple of
is an irrational multiple of ![]() ,
, ![]() is infinite. We next claim that, in this case,
is infinite. We next claim that, in this case, ![]() is a dense subset of C.
We first focus on the special case of x0 = (1,0), and show that x0 is a limit point of
is a dense subset of C.
We first focus on the special case of x0 = (1,0), and show that x0 is a limit point of ![]() . We show that, for any
. We show that, for any ![]() , there is a point,
, there is a point, ![]() , of
, of ![]() whose distance from x0 is less than
whose distance from x0 is less than ![]() .
.![]() . Divide C into N subarcs:
. Divide C into N subarcs: ![]() where
where ![]() . (The reason for using 4/N is to insure that distance between any two points of Ai is less than
. (The reason for using 4/N is to insure that distance between any two points of Ai is less than ![]() . A look at the case
. A look at the case ![]() , N=4 will clarify this point. The number 4 is just a continent choice of a number greater than
, N=4 will clarify this point. The number 4 is just a continent choice of a number greater than ![]() .) Since
.) Since ![]() is infinite, we can find some k such that Ak contains two points,
is infinite, we can find some k such that Ak contains two points, ![]() and
and ![]() , of
, of ![]() .Consider the subset of
.Consider the subset of ![]() ,
, ![]() . Consecutive points of
. Consecutive points of ![]() are a distance less than
are a distance less than ![]() apart, so one point,
apart, so one point, ![]() , of
, of ![]() , must lie in A1, thus
, must lie in A1, thus ![]() .
.![]() . There are a number of ways to show that any
. There are a number of ways to show that any ![]() is also a limit point.
The simplest is to verify that, given any
is also a limit point.
The simplest is to verify that, given any ![]() ,
, ![]() .
. ![]()
![]() ,
function
,
function ![]() is continuous.
We can
derive an infinite set of continuous functions from X to itself, namely
is continuous.
We can
derive an infinite set of continuous functions from X to itself, namely ![]() ,
, ![]() ,
, ![]() , ...
, ...![]() .
.![]() is called the second iterate of f; the composition of n copies of f is called the n-th iterate of f, denoted f(n). We identify f(1) with f.
is called the second iterate of f; the composition of n copies of f is called the n-th iterate of f, denoted f(n). We identify f(1) with f.
![]() , and also have a continuous
function
, and also have a continuous
function ![]() ,
, ![]() . The set of all iterates of x under f is call orbit of x under f.
. The set of all iterates of x under f is call orbit of x under f.
Example 8003
![]() be rotation by an angle
be rotation by an angle ![]() .We can restate the results of Example 0.41 as follows.
Suppose
.We can restate the results of Example 0.41 as follows.
Suppose ![]() . If
. If ![]() is a rational multiple of
is a rational multiple of ![]() , then the orbit of x under f is a finite subset. If
, then the orbit of x under f is a finite subset. If ![]() is a irrational multiple of
is a irrational multiple of ![]() , the orbit of x is dense in S1.
, the orbit of x is dense in S1.
![]()